by ·Ein Kommentar

Mein Name ist Ronald, und ich habe ein ungesundes Verhältnis zu Taschenrechnern.

Seit ich mich vor einigen Jahren mal intensiver mit der Programmierung von Taschenrechnern befasst habe faszinieren mich diese kleinen Computer. Mehr als sie sollten: in meinem Leben finden kaum Berechnungen statt die über die vier Grundrechenarten hinausreichen. Das hält mich nicht davon ab, nach interessanten Geräten ausschau zu halten.

So hat unter anderem auch ein TI-Nspire CAS zu mir gefunden. Die schwarze Variante mit Touchpad, noch mit einem monochromen Display.

Das Service-Menü

Vorhin überkam es mich wieder. Ich habe Batterien eingelegt und mit dem Ding rumgespielt. Der hatte noch die ganzen (trivialen) Berechnungen die ich vor langer Zeit gemacht habe, also hatte ich die Idee einen Firmware-Reset zu machen. Mit einem gewissen Prozedere kommt man in ein Service-Menü, da hat man vier Optionen. Ich wollte gründlich sein und habe in einem Anflug geistiger Umnachtung die einzige genommen die fatal endet: „Complete format (includes operating system)“. Offenbar war es naiv, anzunehmen dass man das Gerät nicht on the fly bricken kann. :-(

Nach etwas Fortschrittsbalken stand auf dem Display nur noch „Operating System not found. Install OS now.“, und mir ging etwas der Puls…

Operating System not found

Das Betriebssystem konnte ich bei Texas Instruments freundlicherweise runterladen (TI-NspireCAS-3.9.0.463.tnc). Die Software die der Hersteller für diesen Fall vorhält (TINspireComputerLink-3.9.0.455.exe) wird aber nur für Mac und Windows angeboten, sowas habe ich nicht. Unter Wine konnte ich das Tool zwar installieren, es hat aber den Rechner nicht gefunden.

Die Lösung war dann ein freies Tool mit dem Namen TiLP. Die Webseite sieht nach nix aus, die letzten News sind von 2013. Aber meine Distribution bringt das als Paket mit, also ist es einen Versuch wert. Und was soll ich sagen? Es hat auf Anhieb den Rechner gefunden, ich konnte die Firmware per Mausklick hochladen.

Nach der Aktion habe ich jetzt nicht nur einen frisch zurückgesetzten Taschenrechner, sondern sogar einen mit dem aktuellsten Betriebssystem — und frisch zurückgewonnenen Respekt vor dem Ausdruck „complete format“… :-/

by ·Keine Kommentare

Diesen Artikel habe ich erst 2015 aus dem alten CMS übernommen, der war 2012 noch nicht im Blog.

Ich weiß ehrlich gesagt nicht woher mein Faible für Taschenrechner kommt. Ich bin kein Mathematiker, und ehrlich gesagt kann ich mir auch nur den Bruchteil der Funktionen eines ‚großen‘ Taschenrechners schlüssig erklären. Aber die Dinger verarbeiten Einsen und Nullen, also muss auch da mal programmiert werden. :-)

Auf Rechner des Herstellers Hewlett Packard bin ich seinerzeit durch einen Emulator auf meinem Nokia N800 aufmerksam geworden. Der heißt Free42, und den gibt es für jedes halbwegs gängige Betriebssystem. Ungewohnt war erstmal die umgekehrte polnische Notation (RPN), das war ein Konzept das ich verstehen wollte. Der Gedanke mir so einen Rechner als Original zuzulegen ist in dem Moment gestorben als ich gesehen habe dass das emulierte Modell — ein HP-42S — immer noch für weit über 150 Euro den Besitzer wechselt. Gebraucht, wohlgemerkt. Der wird seit 1990 nicht mehr hergestellt. Das macht neugierig…

Nun denn, zum Spielen reicht sicher auch die Emulation. Und da ich — außer einem Basic-programmierbaren Sharp PC-1402 Anfang der 90er — nie einen programmierbaren Taschenrechner hatte musste auch das mal ausprobiert werden.

HP-42S

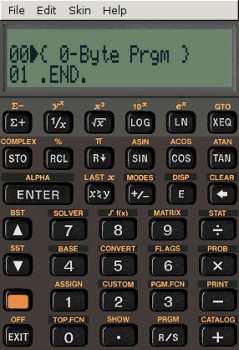
Free42 auf Linux

Free42 auf Linux

Zufällig hatte ich auch gleich ein passendes Problem für die Lösung: zur Zeit arbeite ich in einem Unternehmen in dem Kaffee mit der Geldkarte bezahlt wird. Also mit dem Chip auf der Bankkarte, den man vorher mit Geld aufladen muss. Aufladen kann man nur um ganze Euro-Beträge. Ein Kaffee kostet aber 26 Cent, und ich würde die Karte gerne sauber ‚leer trinken‘. Also muss ich zu meinem Restbetrag den passenden ganzzahligen Euro-Betrag finden damit eine Summe zustande kommt die sich durch 26 Cent teilen lässt. Ein Mathematiker kann das sicher in eine Formel gießen. Wie gesagt: ich bin keiner.

Auf dem Gerät arbeitet man in der Programmiersprache FOCAL, also giesse ich das Problem in ein Programm:

Dieses Programm ist alles andere als perfekt, reichte aber um mir zu zeigen wie man auf so einer merkwürdigen Hardware programmiert. Zur Funktionsweise: zunächst wird die Zahl 0 in Speicher 01 gespeichert. ‚LBL B‘ ist eine Sprungmarke. Dann wird der Wert aus Speicher 01 geholt, um 100 inkrementiert und wieder zurückgeschrieben. Der Wert steht jetzt noch bereit. Mit ‚2 +‘ wird 2 addiert (wir erinnern uns: umgekehrte polnische Notation. Zur Zahl 2 später mehr.), mit ’26 /‘ wird durch 26 Cent geteilt. Vom Ergebnis wird Modulo 1 gezogen. Ist das Ergebnis ungleich 0 wird zu Label B gesprungen, ansonsten wird der aktuelle Wert aus Speicher 01 geholt und durch 100 geteilt. Übrig bleibt der zu ladende Betrag in Euro.

Sicher kann man hier vieles verbessern. Die Zahl 2 ist der Restbetrag in Cent den ich noch auf der Karte habe, so eine ‚Magic Number‘ im Programm ist nicht schön. Außerdem kann es passieren — wenn ich beispielsweise doch mal 25 Cent am Parkautomaten investiert habe — dass mein Restbetrag eine ungerade Zahl ist. Da kann ich Euros addieren bis ich schwarz werde: es wird keine Summe rauskommen die glatt durch 26 Cent teilbar ist.

Aber immerhin: ich kann behaupten, schon einen Taschenrechner programmiert zu haben. :-)

HP-48G

Mein HP-48G

Mein HP-48G

Das hat eine Weile vorgehalten. Irgendwann hat mich das Fieber aber wieder gepackt, ich glaube weil ich für mein Android-Handy andere Emulatoren gefunden habe. Mit Droid48 oder go48g kann man einen HP-48G emulieren. Unter Linux nimmt man x48 um zu spielen.

Der 48G hat gegenüber dem 42S eine Reihe von Vorteilen, einer der gewichtigsten dürfte der weitaus geringere Anschaffungswiderstand der Hardware sein. Das Ding wurde zwischen 1990 und 2003 produziert, 2012 habe ich 30 Euro für einen gebrauchten bezahlt.

Also das gleiche Problem nochmal:

Na das sieht doch schon deutlich weniger nach Assembler aus. Die Sprache nennt sich Reverse Polish LISP (RPL) und wirkt auf den ersten Blick wesentlich erwachsener. Auf den zweiten Blick fallen Zeilen auf in denen sehr merkwürdige Folgen von Variablen, Konstanten und Operatoren stehen. Aber auch eine Abbruchbedingung wie

lässt sich erklären. Wenn man die umgekehrte polnische Notation im Hinterkopf hat und lange genug drüber nachdenkt kommt man in etwa bei sowas raus (mit reichlich Klammern, um wirklich eindeutig zu sein:

Wenn also in der Schleife der zu ladende Betrag grösser als 100 Tassen wird, oder die Summe aus Rest- und Ladebetrag ohne Rest durch 100 teilbar ist wird abgebrochen.

Zugegeben: ich hätte vielleicht auch übersichtlicher programmieren können. Aber etwas Spaß muss ja auch dabei sein, oder? :-)

Und weiter?

Mein TI-Nspire

Mein TI-Nspire

Ich habe hier noch einen Rechner, günstig geschossen während ich auf der Suche nach dem HP-48G war. Das ist ein TI-Nspire von Texas Instruments. Der arbeitet zwar per Default nicht mit umgekehrter polnischer Notation, zeichnet sich aber durch andere Eigenschaften aus.

Als erstes fällt wenn man das Ding in die Hand nimmt das Display auf. Riesengroß, und mit einer Auflösung von 320×240 Punkten. Das schreit geradezu danach, darauf Grafiken zu plotten. Diese Auflösung macht auch eine richtige grafische Benutzeroberfläche möglich. Die ist zwar etwas gewöhnungsbedürftig, funktioniert aber nach einiger Zeit wirklich gut. Darin enthalten sind dann sogar komplexere Anwendungen, wie zum Beispiel eine Tabellenkalkulation.

Auf dem Foto ist auch zu sehen dass dieses Modell über zwei Tastaturen verfügt. Wenn man gerade mal einen ‚einfachen‘ wissenschaftlichen Taschenrechner vorzieht steckt man einfach die zweite Tastatur in das Gerät. Deren Layout ist dem TI-84 plus nachempfunden, und sobald man einschaltet wird eben dieser emuliert. Vollständig. Einschliesslich der vergleichsweise dürftigen Displayauflösung. :-)

Programmiert habe ich diesen Taschenrechner noch nicht. Dabei verspricht das, spannend zu werden: als TI-84 plus unterstützt das Ding TI-Basic, als TI-Nspire sogar die ausgewachsene Skriptsprache Lua — die der eine oder andere vielleicht sogar vom großen Computer her kennt…

Siehe auch…

by ·4 Kommentare

Mein HP-48G

Mein HP-48G

Aus unerfindlichen Gründen bin ich fasziniert von Taschenrechnern. Also weniger vom guten alten TI-30, mehr von den etwas komplexeren Geräten. Ich habe ein paar nette Emulatoren zum spielen gefunden, und mir sogar zwei ‚große‘ gekauft. Einen HP-48G und einen TI-Nspire.

Heute habe ich mal was zu dem Thema auf der Schatenseite veröffentlicht. Das ist — ähnlich wie Mikrocontroller oder Smartphone — wieder eine komplett neue Plattform zum Programmieren. Andere Sprachen, andere Herangehensweise. Ich bin da alles andere als ein Experte. Bis jetzt zumindest. Aber was ich bislang gesehen habe hat mir schon gefallen. :-)

by ·3 Kommentare

HP-42S mit Original-SkinOK, als ‚Fortgeschrittenen‘ würde ich mich im Bereich Mathematik nicht sehen. Absolut nicht. Ich kann nicht mal mehr schriftlich multiplizieren, geschweige denn dividieren. Aber dafür weiß ich wie man einen Taschenrechner bedient. Dachte ich… :-)

Bislang habe ich auf dem Computer immer gcalctool benutzt. Das ist übersichtlich und kann eigentlich alles was man so dauernd braucht. Zufällig habe ich vor ein paar Tagen einen Emulator für einen real existierenden Taschenrechner gefunden. Emulator? Für einen verdammten Taschenrechner?!? Ja, genau. Free42 heißt das dann.

Bei dem Vorbild handelt es sich um das Modell HP-42S, das wurde 1988 von Hewlett Packard vorgestellt und — ich glaube — bis 1994 gebaut. Das Ding findet man natürlich im Taschenrechner-Museum von HP, aber auch in der Wikipedia. Ein programmierbarer Taschenrechner, Umgekehrte polnische Notation, etwa 600 eingebaute Funktionen und 7200 Bytes Platz für eigene Programme. Ich weiß nicht warum, aber das hat mich irgendwie fasziniert. Und nicht nur mich: bei Online-Versteigerungen wird das Ding offenbar teilweise mit über 200 Euro gehandelt. Das ist deutlich mehr als der originale Verkaufspreis vor 15 Jahren, als man das noch im Laden kriegen konnte. Der lag soweit ich weiß bei 130 Dollar.

HP-42S PlatzsparenderWie sieht jetzt so ein Taschenrechner-Programm aus? Was kann man damit machen? Man kann damit eine ganze Menge tun, wie man schnell sieht wenn man sich ansieht was es an Beispielen im Netz gibt. Ich habe mir mal das Alternative Manual durchgelesen und losgespielt. Ein Beispiel muss her…

Das erste was ich benutzt habe ist die Solver-Funktion. Dabei programmiert man eine Funktion mit mehreren Unbekannten (z. B. das Ohmsche Gesetz: U=R*I) die man umgestellt hat so dass 0 rauskommt (also U-R*i=0). Dann kann man die Variablen der Reihe nach mit Werten belegen und den unbekannten berechnen lassen. Man gibt also Spannung und Strom an die für eine LED benötigt werden und kriegt direkt den Widerstand, ohne selbst zu rechnen. Oder Man gibt den gewünschten Strom und den Widerstand an und bekommt die Spannung an der das betrieben werden muss. Nett, aber trivial. Ein komplizierteres Beispiel muss her…

Die Aufgabenstellung habe ich aus einem Podcast ueber Leonhard Euler, allerdings habe ich als Laie wohl was falsch verstanden. Wahrscheinlich ging es um die Euler-Mascheroni-Konstante oder um das Basel-Problem, mein Programm ist vermutlich total uninteressant. Trotzdem taugt es als Beispiel. Die Aufgabe besteht darin, die Kehrwerte von ganzen Zahlen zu addieren. Also 1/1 + 1/2 + 1/3 + 1/4 und so weiter. Mittlerweile weiß ich, dass man das auch mit Logarithmen berechnen kann, aber wie angedeutet würde ich da von alleine nicht drauf kommen.

LBL "EULER"
STO 01
0
STO 02
RCL 01
LBL A
1/x
STO+ 02
RCL 01
1
-
STO 01
x>0?
GTO A
RCL 02

Das Programm arbeitet wie folgt:

  • aktuellen Wert des X-Registers (also die letzte eingegebene Zahl) in Speicher 01 sichern
  • 0 in Speicher 02 schreiben
  • Speicher 01 wieder herstellen
  • Sprungmarke A setzen
  • von der wiederhergestellten Zahl den Kehrwert bilden und zu Speicher 02 addieren
  • Speicher 01 wieder herstellen
  • 1 subtrahieren und den neuen Wert wieder in 01 speichern
  • wenn der Wert groesser 0 ist, nach A springen
  • ansonsten das Ergebnis aus Speicher 02 anzeigen

Also quasi folgendes, nur halt im Taschenrechner (und nicht nur fuer 100):

perl -e "$j=0;for($i=1;$i<=100;$i++){$j+=1/$i};print$j;

In einer Tabellenkalkulation habe ich das auch mal gemacht um die Werte zu kontrollieren, aber da kann man das (ohne wirklich zu programmieren) nur bis knapp ueber 60.000 machen, weil dann die Tabelle am Ende ist. Das Ergebnis fuer 999.999.999 ist 21,3004815013 (da hat der Taschenrechner aber auch eine Weile drauf rumgekaut).

Ich bin einfach mal weiter fasziniert, vielleicht konnte ich ja irgendwen anstecken… ;-)